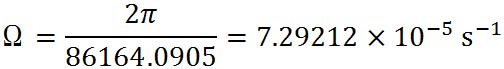コリオリの力 (3)
これまで2回の説明で、コリオリの力を求める準備は整った。ニュートンの運動の第2法則から、力は質量と加速度の積であり、コリオリの加速度が分かれば、それに物体の質量を掛け合わせることでコリオリの力は求められる。
前回求めたコリオリの加速度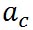 は、 は、
であった。ここで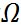 は地球の自転の角速度で、 は地球の自転の角速度で、
である。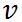 は物体の速度である。この式から、コリオリの加速度は、物体の速度に比例する。そのため、物体の速度が0であれば、すなわち静止した物体にはコリオリの加速度は作用しない。 は物体の速度である。この式から、コリオリの加速度は、物体の速度に比例する。そのため、物体の速度が0であれば、すなわち静止した物体にはコリオリの加速度は作用しない。
地球のような球体では、緯度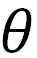 におけるコリオリの加速度の地表に水平な成分は、 におけるコリオリの加速度の地表に水平な成分は、
同じく、コリオリの加速度の地表に垂直な成分は、
となる。緯度と速度を変化させて、これらの加速度の値を計算してみよう。
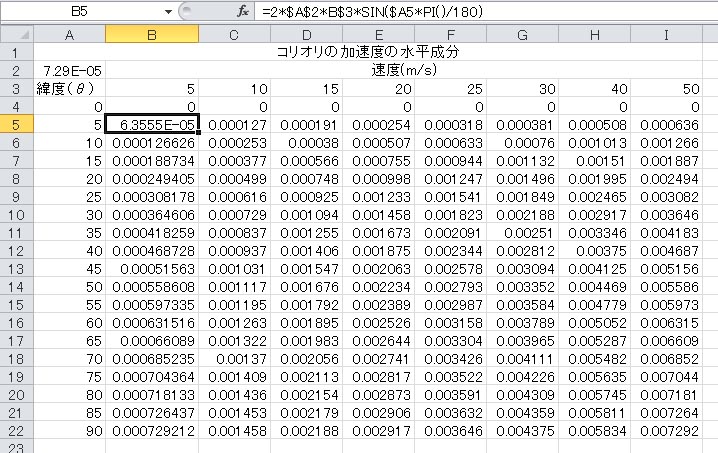
エクセルで緯度0度(赤道)から90度(極)まで、緯度を5度ずつ変化させて計算したコリオリの加速度の水平成分の計算結果の表を示す。速度は5 m/s から50 m/sまで変化させている。気象学で扱う通常の風速は、この程度の値の範囲である。数式バーに示されている計算式を、軸となるセル以外のセルにすべてコピーすれば計算は完成する。
緯度0度では、コリオリの加速度は0であり、緯度が増加するとすべての速度で、それにしたがってコリオリの加速度は次第に増加して行く。
グラフにすると以下のようになる。このグラフの形はサインカーブそのものである。
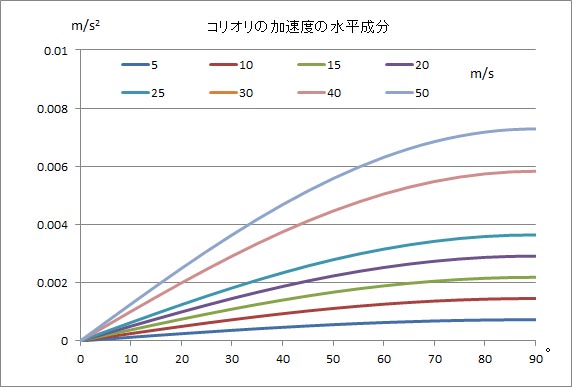 |
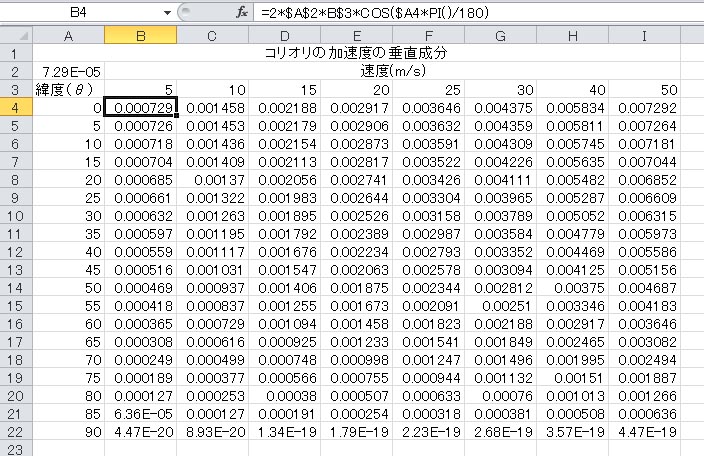
同様にして、エクセルで計算したコリオリの加速度の垂直成分の計算結果の表を以下に示す。計算式は数式バーに示されているものを、軸となるセル以外のセルにすべてコピーすればよい。
コリオリの加速度(力)は赤道では0であるというが、これは地上に水平な成分のことを言っているのであって、冒頭に示したコリオリの加速度は地球の自転軸に垂直に作用しており、これは赤道上で0ではない。したがって、コリオリの加速度の地表に垂直な成分は、赤道上でも0ではなく、逆にすべての緯度の中で一番大きな値となっている。
極におけるコリオリの加速度の値が微小量となっているが、これはエクセルにおける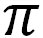 の打切り誤差と考えられ、正しくは0となる。 の打切り誤差と考えられ、正しくは0となる。
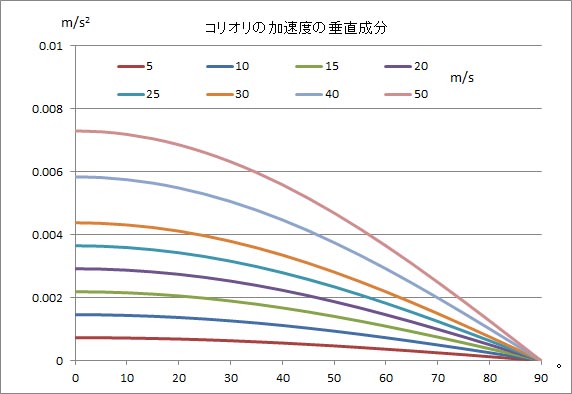
グラフにすると上のようになる。このグラフの形はコサインカーブそのものである。赤道上でコリオリの加速度は最大であるが、それでもコリオリの力 (1)で計算した地球の自転による遠心力の値より一桁小さい大きさである。よほど高速の物体でない限り、重力加速度の0.1%以下の値にしかならない。
このコリオリの力の垂直成分の大きさについては、小倉気象学に、緯度35度の場所を時速200 kmで東西に走行する新幹線に乗車している体重50 kgの人の体重は、コリオリの力の垂直成分によって重量にして約33 g軽くなる、という例が掲載されている。同様の計算を、時速108 km(秒速30 m)で高速道路を走行する車に乗車する体重 60 kgの人で計算してみよう。
緯度35 °の地点を秒速30 mで東西に走行する物体に作用するコリオリの加速度の垂直成分は、上に示した計算結果の表から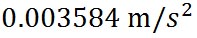 であり、 であり、
となることから、重量にして約22 g軽くなる。
(2011.7.27)
|