|
|
主成分分析 1
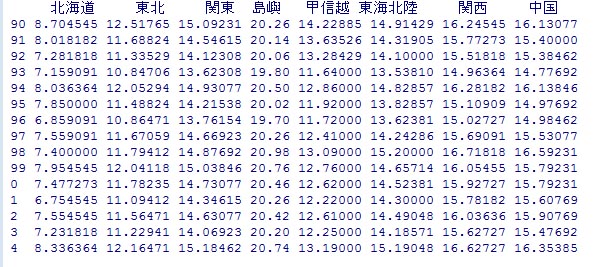
前回の気温の解析から、北海道と東北の気温の関係と北海道と沖縄奄美の気温の関係との間には、異なった傾向があることが分かった。それでは、北海道と関東の関係は?北海道と関西の関係は?と疑問が湧く。この答えを得るために、それぞれの地方別に散布図を描いたり、相関係数を計算したりすることもできるが、各地方の傾向を全体的に眺めることができると好都合である。それには主成分分析が常套手段である。そもそもエクセルではなくRを使うメリットは、Rでは主成分分析が極めて容易にできるからである。
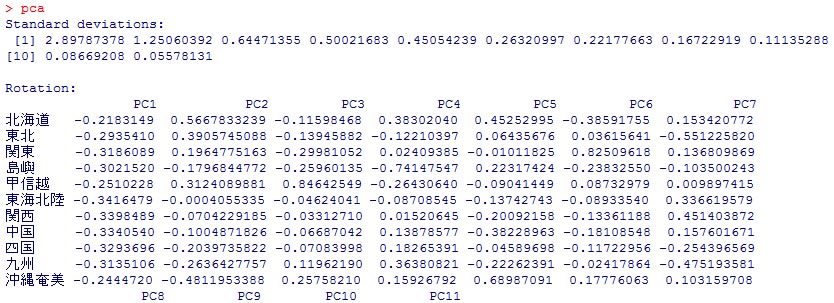
続いて主成分分析を行なってみよう。 pca=prcomp(Temp19902013, scale=T) とすると主成分分析の結果がpcaに代入される。ここでscale=Tはデータの尺度(スケール)の自動調整を行うことを指定したものである。北海道と沖縄では気温の値が異なるが、尺度の自動調整をすると、気温の年々の変動のみに注目することができる。続いて、 pca とすると、各主成分の標準偏差と回転が表示される。ここでは、日本を北海道から沖縄奄美まで合計11の地方に区分して気温の変動を解析した。そのため、第1から第11までの合計11の主成分が計算される。
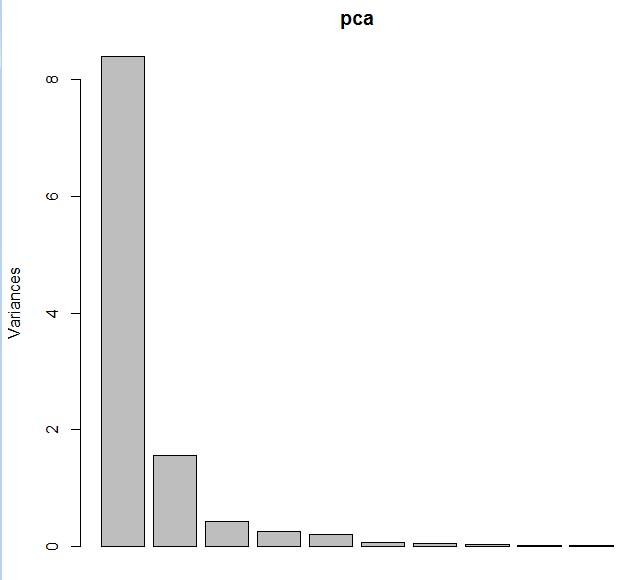
ただ、これを見ても何のことかわからないだろう。この結果をプロットしてみる。それには、 plot(pca) と入力すればよい。すると、下図が表示される。
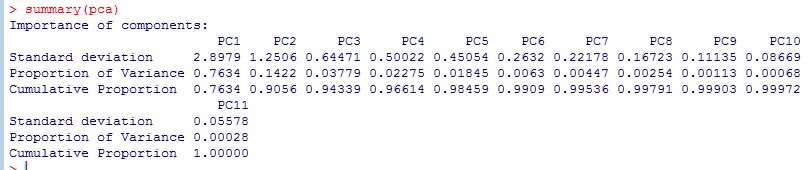
第1主成分の分散が極めて大きく、第2主成分まででかなりの部分を説明できていることがこのグラフから分かる。主成分分析の結果の概要は、 summary(pca) とすると表示される。
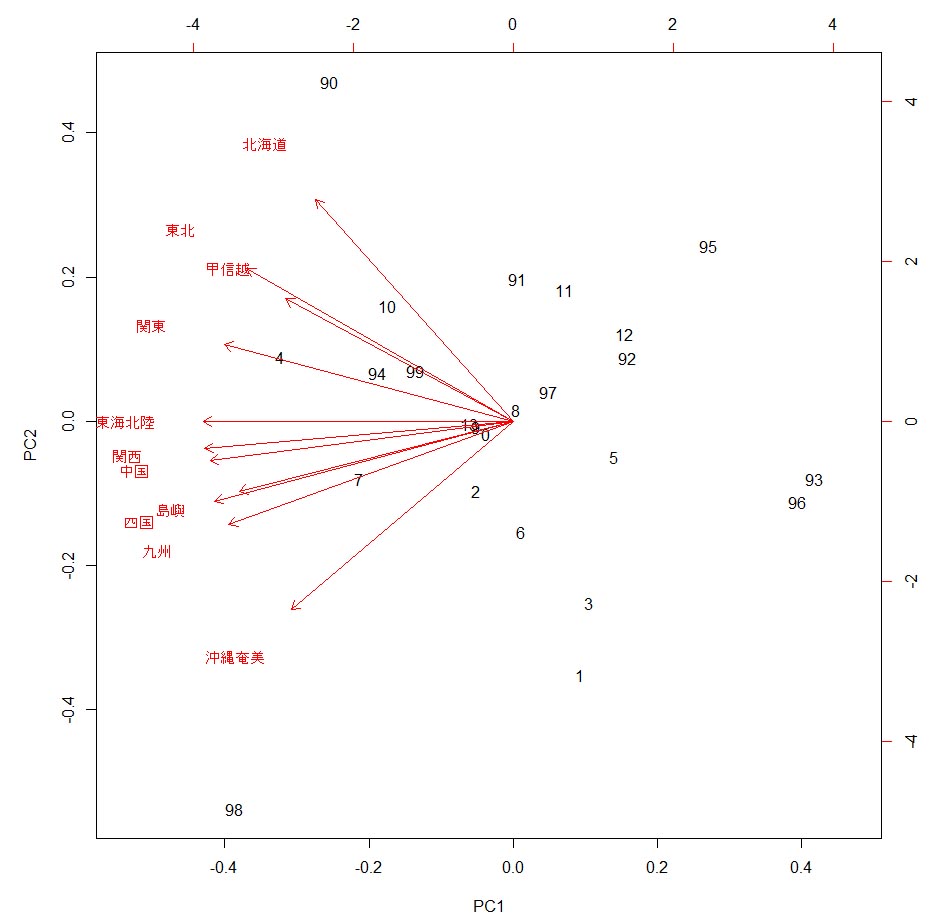
ここに表示されているのは、各成分の重要度(Impotance of compornent)である。PC1、PC2・・・が1から11までの主成分を示し、その下に、標準偏差(Standarad deviation)、寄与率( Proportion of Variance)と累積寄与率(Cumulative Proportion)が示されている。 ここに表示されている結果から、第1主成分の寄与率が76%、第2主成分の寄与率が14%で、第2種主成分までの累積寄与率は約91%となっている。 ここで、第1主成分と第2主成分の意味を考えるには2種類のグラフを重ねてプロットするbiplot関数を用いると分かることがある。 biplot(pca,choices=1:2, scale=1, pc.biplot=FALSE) と入力すると、以下のグラフが描かれる。
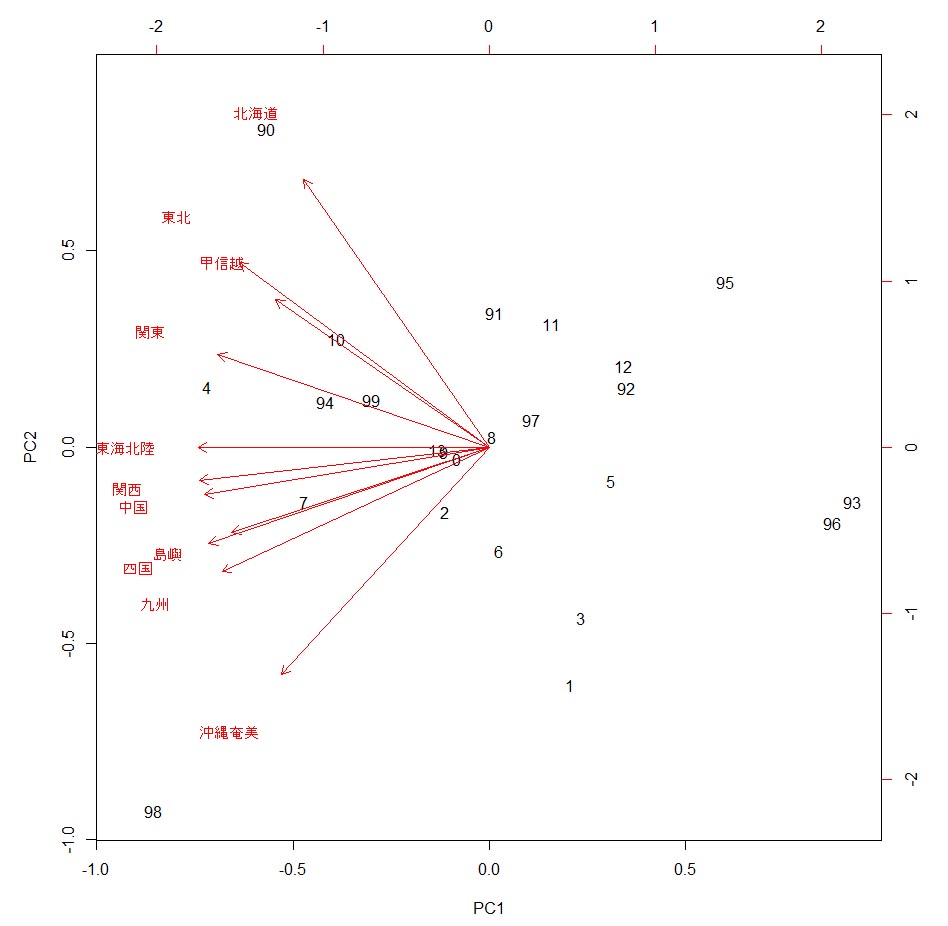
数字は2桁で表した年号、それに地方の特徴を示した矢印と地方名が表示されている。 主成分1で一番左側にあるのが1998年、それから2004年、1990年、2007年の順で左から右に並んでいる。 主成分1で一番右側にあるのは1993年、次いで1996年、1995年と順に右から左に並んでいる。 日本の気温変動についての若干の知識があれば、1993年は気温が低かった年で、1998年は気温が高かった年であることはすぐに分かる。このことから、主成分1は、年平均気温の高低を示した軸と考えてよいだろう。 そして、地方の特徴を示すと見られる主成分2は、きれいに北から南の地方順に並んでいるように見える。このことから考えると、主成分2は日本の地方の南北の特徴を示す軸と考えられる。 これら年と地方の関係をさらに考えると、北海道は1990年の年平均気温が最も高かった。沖縄奄美は1998年の気温が最も高かった。関東は2004年の年平均気温が最も高かった。その年に地方の軸が重なるようにしてみよう。 主成分2のスケールを調整するために、以下のように入力してみた。 biplot(pca,choices=1:2, scale=0.7, pc.biplot=FALSE) すると以下のグラフが描かれる。
沖縄奄美の年平均気温が最も高かった年は1998年で2番目に高かった年は2006年である。一方、九州は、一番高かったのは1998年であるが、2番目に高かった年は2007年である。島嶼は、1998年が最も高かった年で、1999年が2番目に高かった年である。これらの関係から、地方別の矢印の向きが分かるような気がする。 ちなみに、沖縄奄美の気温がこの期間で最も低かった年は1995年であり、関東の気温が最も低かったのは1993年、北海道は1996年であり、いずれも矢印の反対方向に近いところに位置している。 (2014.12.17) | |||||||