ベクトルのドット積
これまで、ベクトルの足し算(加法・加算)と引き算(減法・減算)について説明した。ベクトルには、このほかにも掛け算(積)がある。それもドット積とクロス積の2種類の掛け算がある。初めに、ドット積(内積ともいう)について説明する。
ベクトルは、大きさだけなく方向も持った量であり、二つのベクトルの間のドット積は、それらの大きさを掛け合わせるだけでなく、それらのベクトルがどれだけ異なった方向を向いていかをも考慮している。ただ、ドット積の結果はベクトルではなく、大きさだけをもつスカラーとなる。
ドット積は、二つのベクトルの間にドット(・)を付けて表す。例えば、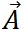 と と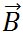 のドット積は のドット積は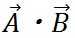 のように表す。そして通常AドットB(エー・ドット・ビー)と読む。 のように表す。そして通常AドットB(エー・ドット・ビー)と読む。
以下、ベクトルの加算の際に用いたベクトルの図を用いて、ドット積について説明する。ベクトルは平行移動しても値は変化しないので、 と と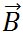 の始点を座標の原点に移動する。 の始点を座標の原点に移動する。
すると、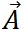 はその終点の座標 はその終点の座標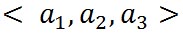 によって表され、 によって表され、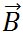 も、その終点の座標 も、その終点の座標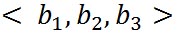 によって表すことができる。これら二つのベクトルのドット積は、これらの成分同士を掛け合わせた上で、それらの和として定義される。これを式で表すと、以下のようになる。 によって表すことができる。これら二つのベクトルのドット積は、これらの成分同士を掛け合わせた上で、それらの和として定義される。これを式で表すと、以下のようになる。
この式から分かるように、二つのベクトルのドット積には方向はなく、大きさだけがあるスカラーである。
ドット積にはもう一つの定義があるが、それをベクトルを平面的に示した図で説明すると以下のようになる。
ここで、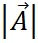 と と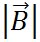 は、それぞれ は、それぞれ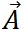 と と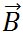 の大きさ(長さ)を示す。θは、 の大きさ(長さ)を示す。θは、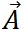 と と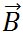 の方向の間の角度である。この式からも、ドット積がスカラーであることが分かる。 の方向の間の角度である。この式からも、ドット積がスカラーであることが分かる。
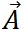 と と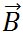 がともに同じ方向を向いていると、θは0となり、 がともに同じ方向を向いていると、θは0となり、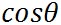 が1となることから、ドット積は が1となることから、ドット積は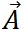 と と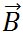 の大きさ(長さ)の積となる。 の大きさ(長さ)の積となる。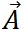 と と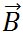 が逆方向を向いている場合は、 が逆方向を向いている場合は、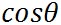 が-1となり、ドット積は が-1となり、ドット積は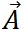 と と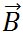 の大きさ(長さ)の積の値を
負にしたものとなる。 の大きさ(長さ)の積の値を
負にしたものとなる。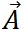 と と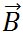 が互いに直角の場合は、ドット積は0となる。、このようにして、二つのベクトルのドット積の値から、それらのベクトルの方向の違いを知ることができる。 が互いに直角の場合は、ドット積は0となる。、このようにして、二つのベクトルのドット積の値から、それらのベクトルの方向の違いを知ることができる。
ここで、ドット積の二つの定義、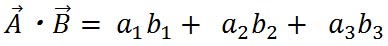 と と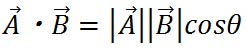 とが同じ値を与えることを確かめてみよう。 とが同じ値を与えることを確かめてみよう。
最初に、特殊な例として、二つのベクトルがともに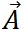 である場合を考えよう。その場合、ベクトルを成分で表して計算するドット積は、 である場合を考えよう。その場合、ベクトルを成分で表して計算するドット積は、
となり、ベクトルの長さの2乗の値となる。一方、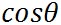 を用いた定義式でも、 を用いた定義式でも、
となり、確かに同じ値を与える。
次に、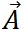 と と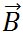 との方向がθの角度をなしている場合について確かめてみよう。ベクトルの減算の中で使用した図を以下に示す。 との方向がθの角度をなしている場合について確かめてみよう。ベクトルの減算の中で使用した図を以下に示す。
上の図で、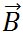 の終点から の終点から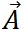 の終点に向かうベクトルは の終点に向かうベクトルは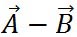 となる。ここで、 となる。ここで、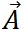 、 、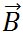 と と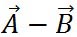 で構成される3角形に第2余弦定理を適用すると、上の図に示した関係が得られる。 で構成される3角形に第2余弦定理を適用すると、上の図に示した関係が得られる。
一方、二つのベクトルをともに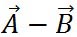 とするドット積は、分配法則を用いて以下の式のように計算されるが、このドット積の値は、 とするドット積は、分配法則を用いて以下の式のように計算されるが、このドット積の値は、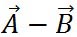 の長さの2乗である。 の長さの2乗である。
ここで、第2余弦定理とドット積の両者によって計算した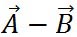 の長さの2乗を等置して整理すると、以下の式が得られる。 の長さの2乗を等置して整理すると、以下の式が得られる。
すなわち、ドット積は二つのベクトルの長さと、それらのベクトルの方向余弦を掛け合わせることによって得られることが示された。
(2011.8.1)
|